Ev Formula Poker
An important concept that most winning Texas holdem players
understand is expected value.
Concept – Expected Value (EV). Expected Value is the probability-weighted average of possible results. EV = Win%. WinAmt - Lose%. LoseAmt. For example, – If Win% = 25% and you are facing a $60 bet into a pot of $100 – EV = 25%. (100+60) - 75%. 30 = 17.5. In general, decision rules will be made based on Expected Value. But when betting or raising yourself, utilizing a complex EV formula is powerful. And let’s be honest, there are very few things in poker that are more fun than shoving. And if you are considering doing more 5bet bluff shoving preflop or semi-bluff jamming postflop, then understanding the math behind it is crucial.
The expected value is the average amount you win or lose on a
situation if you were able to play the exact same situation
thousands of times.
- To calculate your poker equity - or how often you should win a hand, you can use a simple formula. Count how many outs you have. For example, if you're drawing to a flush, you have 13 suited cards, two in your hand, two on the board - leaves 9 outs.
- Formula for Expected Value The first variation of the expected value formula is the EV of one event repeated several times (think about tossing a coin). In such a case, the EV can be found using the following formula.
It can be difficult to understand expected value on a hand
for hand basis, but if you ran a situation 100 times it can help
make it clear.
Here’s an example:
You’re finished with the betting round on the turn and are
waiting for the river card to be dealt. You have four cards to a
flush and if you complete the flush you’ll win the hand and if
you don’t complete your flush you’ll lose the hand. Nine out of
the 46 remaining unseen cards win the hand for you and there’s
$100 in the pot.
The percentages say you’ll win the hand 19.57% of the time.
You can figure the percentage yourself by dividing nine by 46.
If you play the exact same situation 100 times you win 20
times and lose 80 times. We rounded the 19.57% up to 20.
So 20 times you win $100 for a total win of $2,000. If you
divide $2,000 by 100 times you end up with the average win, or
expected value for this situation. In this case the expected
value is $20.
This is a simplified example and isn’t especially useful at
the holdem tables. But if we take the reasoning and mathematics
behind what you just learned a bit deeper you can find a way
expected value can be quite valuable and useful at the Texas
holdem tables.
If you take this example to the next level consider this
situation.
In the same hand after the turn card has been dealt your
opponent bets $20 into a $60 pot, you can use expected value to
determine if you should call or fold.
The cost of the call, $20, is multiplied by 100 to come up
with a total cost of $2,000 to play the situation 100 times. The
20 times you win the hand you win $100. 20 times $100 is $2,000.
So it looks like your expected value is 0 in this situation.
But there’s still one thing to consider. What happens on the
river when you miss your hand and when you hit your hand? If you
don’t check and fold on the river every single time you miss
your hand your expected value goes below even.
Will your opponent ever call a bet on the river if you hit
your flush? The answer is certainly yes. They might not call
often, but you can get action on the river with a flush. This
actually pushes the expected value of a hand like this to the
positive side.
As a Texas holdem player you need to make it your goal to
find as many positive expectation situations as possible and
play in every one of them possible. You also need to avoid
negative expected value situations like the plague.
The magic of positive expectation is the short term results
don’t mean anything. If you consistently put yourself in
positive expectation situations you’ll win money in the long
run.
Statistical laws show you have to make money in the long run
if you always play in positive expectation situations.
Here’s a list of a few positive expectation situations:
- Getting all in pre flop with a better hand than your opponent. Different
hand strengths have different positive expectation spreads, but
any advantage will pay off in long term profit. Pocket aces have
a huge positive expectation over seven two off suit, but even a
nine seven off suit has a long term advantage over eight six off
suit that pays off over time. - Calling small bets in comparison to the pot size when you a flush draw,
open end straight draw, or other strong draw. - Playing in a game filled with players who aren’t as good as you. It’s
difficult to determine an exact expected value amount in this
situation but it’s profitable. - Leaving a table immediately when you realize every other player is better
than you. You don’t win money in this situation, but you lose
less so it’s a positive play.
Expected value is often shortened to EV. You may see positive
expected value listed as +EV or negative expected value listed
as –EV.
One of the biggest mistakes Texas holdem players make when
trying to wrap their head around expected value is trying to
figure out how the money they’ve already placed in the pot gets
figured into the equation.
The answer is simple, but most players have a hard time with
it. The money you’ve already put in the pot is only considered
in the pot size. In other words, the money stops being yours as
soon as it goes in the pot.
If you make a positive expected value play on every decision
of the hand everything else will take care of itself.
Examples of Expected Value
The best way to learn how to determine expected value in
Texas holdem is to practice. This section includes many examples
so you can practice for free. When you practice at the tables it
can cost you money.
Take a few minutes and try to figure out the correct answer
before looking at the solution. Remember to run the situation as
if it was identical 100 times. Just follow the simple steps used
in the opening section.
The examples all come first and the solutions are further
down the section. This way you can’t cheat to see the answers
before you try to figure out the answers unless you want to. All
of the examples are using Texas holdem.
Example 1
On the river of a no limit game you have the top pair with a
good kicker but only think you have a 20% chance of having the
winning hand. The pot has $500 in it, you check, and your only
opponent bets $250.
Example 2
You’re playing a $10 / $20 limit game and after the turn you
have an open end straight draw and a flush draw. The pot has
$100 in it, you check and your opponent bets $20.
Ev Formula Poker Odds
If you raise your opponent will call on the turn and call one
bet on the river if you hit your straight, but will fold to a
bet if you hit your flush. If you miss your draws you check and
fold to a bet on the river.
Example 3

On the river of a no limit game the pot has $2,000 in it and
you just hit a full house on a board that has three suited
cards. The way the hand played out you’re relatively sure your
opponent hit the flush. You have to act first and are trying to
determine the best way to extract the maximum expected value
from the situation.
You can check and raise if your opponent bets or you can bet.
The mounts of bets and raises complicate the situation, but
being a winning Texas holdem player is complicated, so you have
to make your best educated guess when situations like this come
up.
Based on what you know about your opponent if you make a bet
up to $2,000 she’ll call. If you check she’ll bet $500 and call
up to a re-raise of $1,000.
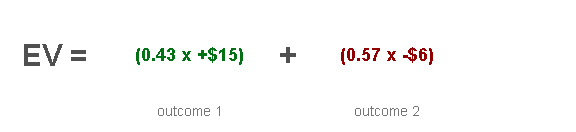
Example 4
You’re playing in a $20 / $40 limit game and flop an open end
straight draw. The pot has $80 in it at the start of the round,
the first player bets, the second folds, the third calls, and
you’re last to act. The pot now has $120 in it and you have to
call a $20 bet to see the turn.
played figure into your decision?
Example 5
After the river has been dealt you have top pair and top
kicker. You determine you have a 40% chance of winning the hand
because the way the hand has played out your opponent either has
top pair with a worse kicker or hit two pair. Your opponent has
played the hand aggressively enough that you’ve tilted the
percentage to her favor.
The pot has $1,000 in it before your opponent bets $800. Once
you know the break-even expected value it’s easy to see if a
call or fold is more profitable in the long run.
If your percentage is correct what’s your expected value if
you call?
How much would your opponent have to bet to make your call a
break even expected value?
Solution 1
If you call $250 100 times your total investment is $25,000.
The total amount of the pot is $1,000 after you call. Winning
20% of the time means you win a total of $20,000 when you win.
This is a negative expected value of $5,000 total and $50 on
average.
You need to win this hand at least 25% of the time to break
even. You know this because the total investment stays the same,
creating a total amount of $25,000. You divide this by the size
of the pot to find the break-even point. $25,000 divided by
$1,000 is 25, so you need to win 25 out of 100 times, or 25%.
Solution 2
Ev Formula Poker Calculator
This situation has a host of possibilities so you need to
consider them one at a time. Before moving deeper you need to
decide if a fold or call is correct.

You’re faced with a call of $20 making a total pot of $140.
You have 15 outs out of 46 unseen cards for a percentage of 33%
chance to win. Your total investment over 100 hands is $2,000
and the 33 hands you win return $4,620. This creates an average
positive EV of $26.20 per hand. So you can rule out a fold.
Now let’s consider a raise. Three things can happen if you
raise, so you need to consider each of them and then combine the
results.
The first thing that can happen is you raise, your opponent
calls, and you miss your draws. Your raise costs $40 so over 100
hands you lose $4,000, or $40 on average. This happens 31 times
out of every 46 possibilities, or 67 times out of 100.
The second possibility is you raise, your opponent calls, you
hit a flush, and you don’t win additional money on the river.
Over 100 hands your raise still costs $40, making a total pot of
$180. You win $180 100 times for a total win of $18,000. When
you subtract your investment of $4,000 you have a positive
expectation of $14,000. This is an average of $140 per hand. You
hit your flush 20 out of 100 hands.
The third possibility is you hit your straight. In this case
you bet $40 on the turn and another $20 on the river for a total
investment over 100 hands of $6,000. The total pot size after
all betting on the river is $220, for a total win of $22,000.
This is an average win of $160 per hand. You hit your straight
and not a flush 13 out of 100 hands.
When you combine the results you have the following:
- 67 times out of 100 you lose $40.
- 20 times out of 100 you hit your flush and win $140.
- 13 times out of 100 you hit your straight and win $160
- 67 times 40 = a loss of $2,680
- 20 times $140 = a win of $2,800
- 13 times $160 = a win of $2,080
This makes a total positive expected value of $2,200,
creating an average of a $22 +EV per hand.
When you compare this to the +EV of $26.20 per hand created
by calling it shows both options are profitable but a call is
correct in this situation.
Realize that if you can extract more money on the river than
in this example a raise may increase to a point where it has the
higher EV.
Solution 3
In the first situation a bet of $2,000 in 100 hands is a
total investment of $200,000. The total pot size with your
opponents call is $6,000, for a total win over 100 hands of
$600,000. This is a positive expectation of $400,000 over 100
hands for an average of $4,000.
The second situation requires a total bet of $1,500, covering
the $500 bet and the $1,000 raise. This makes a total investment
of $150,000 over 100 hands. The total pot size is $5,000 so the
total win over 100 hands is $500,000. This creates an expected
average value of $3,500.
So the correct play is to bet $2,000.
This may seem like a simplified example, but this is a
perfect example of the complicated situations you fin at the
holdem tables on a regular basis. When you start considering all
of the possible outcomes for each hand being able to determine
expected value goes a long way to maximizing your long term
profit.
Solution 4
The first thing to determine is the expected value from the
flop to the turn. You’ve seen five cards so the deck has 47
unseen cards and eight of them complete your straight. This
means that 17% of the time you’ll complete your straight on the
turn.

It costs you $2,000 to call the $20 bet 100 times and the 17
times you win the total amount won will be $2,380, assuming no
further action in the hand.
But the odds of no further action taking place in the hand
are slim. Also, what happens if you miss your draw on the flop?

Unless the expected value is close to even you don’t need to
determine how likely you’ll get additional action is when you
hit. If the EV is close to even or slightly negative the
expected future action is enough to push the percentages to make
a call correct. That’s all you need to know to continue with the
hand based on possible future action.
The next thing to consider is what happens when you miss your
draw on the turn. The pot is now $140 and the bets are $40. The
only way you’d ever consider folding in this situation is if you
get caught in a bidding war between the other two opponents, and
even then with capped betting rounds the expected value says to
call.
More likely you’ll face a single bet or two bets at most. The
first thing you need to do is determine if the situation still
offers a positive expectation if you face two bets.
Ev Formula Poker
Two bets from each of your opponents make the pot $300 and
you have to call $80, making a total pot size of $380.
You’ve now seen six cards, leaving 46 unseen and you still
have eight outs. Your percentage chance of winning has improved
slightly but it still rounds down to 17%.
Your total cost to call 100 times is $8,000. The 17 times you
win you get $380, for a total win of $6,460, creating a negative
expectation situation of $15.40 on average.
This is where you need to make a judgment call based on how
much you think you can extract from your opponents on the river
when you hit your hand. You need to win an average of $470 total
instead of the $380 listed above to break even, so can you get
over two additional bets on the river when you hit?
An open end straight draw is harder to see when it hits for
your opponents than a flush, and you’re in good position, so you
can probably push your wins enough when you hit to make this a
break even play or a slightly positive EV play. But it’s close,
so it really helps to know your opponents.
What about if you only face a single bet from each of your
opponents?
In this case you have to call a $40 bet and the size of the
pot is $260 with both opponent’s bets and your call. It costs
$4,000 for 100 calls and the 17 times you win the total amount
is $4,420. This is a positive expected value and is a clear
calling situation. You’ll actually win more when you hit your
hand in most situations from action on the river.
The last thing to think about is if you should actually raise
on the flop.
If you raise what will your opponents do? To get a true
picture you need to run every possible situation, but for the
sake of this discussion let’s assume one opponent folds and the
other calls.
The pot has $120 in it, you raise $40, and the remaining
opponent calls $20 for a total pot of $180. Your raise in 100
hands totals $4,000 and you still win 17 times. 17 times $180 is
only $3,060, creating a negative expectation situation.
When you factor in the possibility of both opponents folding
and winning more bets on the turn and river when you hit it
still isn’t enough to make a raise enough. Remember that
sometimes your opponent will re-raise, making the situation
worse.
This is a complicated example so if you don’t understand all
of it, take the time to go back over it and study it. None of
the calculations are overly complicated, but it can be confusing
when you run into so many of them.
Solution 5
It’s going to cost you $800 to call, so you multiply that by
100. So your total cost is $80,000. The 40 times out of 100 that
you win you’ll win a pot of $2,600. 40 times $2,600 is $104,000.
So the total amount of your wins minus the cost of making the
call is $24,000. If you divide this by 100 your average expected
value is $240 every time you’re in this situation.
To determine the break even amount your opponent would need
to bet requires a slightly different calculation. Your opponent
would need to bet $2,000 to create a situation where your
expected value is zero.
Ev Formula Poker Table
A bet of $2,000 costs $200,000 to call 100 times. The pot is
$5,000, so when you win 40 out of 100 times you win a total of
$200,000, creating a zero expected value.
This means that any bet below $2,000 in this situation has a
positive EV to call.
More importantly, consider how important it can be to call
almost every bet on the river if you have a 40% chance to win.
You can work these numbers for any percentage chance of winning
to determine if a situation offers positive or negative EV. Most
players fold too often to small and medium bets on the river.
You can use a complicated mathematical formula to determine
this amount, but it’s simpler for 99% of the population to do a
simple progression of possibilities.
Here’s exactly how we determined that a $2,000 bet is the
break-even point.
We know that a bet of $800 creates a large positive
expectation situation so a break-even will need to be quite a
bit larger than that. So we built a small table and started
plugging in bets.
| Bet Amount | Total Pot | Call X100 | 40 Wins X Pot | Average EV |
|---|---|---|---|---|
| $1,000 | $3,000 | $100,000 | $120,000 | $200 |
| $1,500 | $4,000 | $150,000 | $160,000 | $100 |
| $2,000 | $5,000 | $200,000 | $200,000 | $0 |
Don’t be scared or intimidated by these calculations. Once
you do a few of them you’ll quickly learn they aren’t too
difficult. Pick a different situation and build a table to find
the correct break-even point.
You need to practice these quite a bit so you learn to
closely approximate your expected value at the table. It’s
difficult to determine all of this in your head, but as you gain
experience you’ll learn to recognize profitable and unprofitable
situations.
Summary
Expected value is just one of the many tools that winning
Texas holdem, players use, but it’s an important one. Winning
players strive to fin and exploit positive EV plays. If you can
enter more positive plays than negative ones you’re well on your
way to a long term winning career.
Go over the examples on this page and practice the
calculations every chance you get until it becomes easy. It may
be difficult at first but if you stick with it you’ll be glad
you did and it’ll pay for itself for years to come.
Expected Vaue (EV)
You may have heard of the EV concept (expected value) in the past, especially if you play poker. It is a very important probability mathematics concept that applies to all gambling games, and even most real life situations. But what is it? In short, EV is the expected value returned on any wager. You can use the expected value concept in Poker, sports betting, casino games like Blackjack, slot machines, roulette... you name it.
This article targets players who want to understand the mechanics of gambling. If you are a player that just likes to have fun, such a concept will be pretty boring for you. It will explain in more details what expected value is, why you should care, how it works and how to use it in gambling. We will explore its use in Poker, Casino games and Sportsbetting. After getting this basic knowledge, you will be able to read more and understand what people are talking about.
Note that since most readers aren’t math fiends, the article aims to teach the basics of expected value, the tools we can all use easily while playing. You can even use what you learn in this article in your real life everyday situations.
What is EV (expected value) and why should I care?
In gambling, you are constantly faced with situations where you have multiple options, the first of which is to decide which game you’re going to play. Each choice you encounter causes different outcomes based on the option chosen. The concept of expected value (EV) is precisely used to evaluate which option you should choose to maximize gains and minimize losses. It excludes variables like fun or personal satisfaction. Expected Value (EV) is essentially a positive (+EV) or negative (-EV) indicator that should guide you in making the best decision.
Before getting into the details, let’s use an example that will demonstrate how expected values work. Say you and a friend are flipping a coin and decide to bet on the outcome. All things being equal, each face of the coin should be randomly selected 50% of the time. But you’re a wise entrepreneur and you manage to convince your friend that each time he wins, you give him 0.98 cents while when he loses, you earn the full amount. Here is what the formula would look like:
Expected value (EV) = wager + (expected win – expected loss)
In this scenario, on your point of view, it would look like this:Expected value (EV) = 1 + ((0.5 x 1) – (0.5 x 0.98)) => 1.01
In other words, for you the expected value of wagering 1 unit of money is equal to 1.01, an average profit of 0.01 per coin flip. The EV of this wager is positive and favorable. Of course, in this case the profit is negligible. Similarly, the loss for your friend would be small since statistically, he would get 0.99 back on every coin flip. But when it comes to real gambling, expected value matters because it is the difference between winning and losing. This was a very simple example.
Since you will be playing more than 1 coin per wager, and the house / player edge will be more than 1% (compounded by the number of times you make this wager), it can amount to thousands of dollars. We hope this convinces you of the importance of the Expected Value (EV) concept. When the expected value of a bet is positive, then it means that statistically, in the long run you should make money. If it’s negative, then it means that you will lose money.
When does Expected Value (EV) matter?
The concept doesn’t matter much when you play a game for fun and you don’t mind losing. If you like playing American Roulette, the one with 0 and 00, then you have approximately 0.95 EV (expected value) on any given wager you can make. That is, on average, for every 1 unit of currency wagered, 0.95 will come back.
It is the house advantage. This edge varies from game to game but it is always in the casino’s advantage, and this is why there is a saying that the casinos always win. The longer you play, like in the coin flip example, the more money they make. Or if you were on a lucky streak in the first flips, the longer you play and the more likely you will lose what you had gained.
Can the Expected Value ever be in the player’s favor? Indeed, it can be in games involving not only luck but also skill. There are 4 occurrences where this is the case:
1. Poker, where an experienced player can and should win in the long run.2. Sports betting, where a good handicapper can also have an edge over the house.
3. Blackjack, where card-counting can increase your expected value to about 1.02 but it is considered cheating.
4. Games in which there is a progressive jackpot.
Those are to our knowledge the only games where skill can be used to increase Expected Value (EV) above 1, making every dollar played an investment instead of a loss. The other games are for fun. We will now give very basic examples on how this applies to Poker and Sportsbetting.
Sportsbetting Expected Value (EV)
Expected value in sports betting involves the same sort of calculations, with a twist: you know the house edge but don’t know your real odds of winning and losing. This is where knowledge and experience come into play. You have to estimate them adequately. If you manage to do this, you can beat the odds.
Say that in the Premier League, team A is playing team B. The odds given by the bookie for team A is 4/1 (4.0 in decimal, +300 in american). But you know both teams really well and you estimate that team A will win 50% of the time. Your expected value (EV) in betting on team A would be positive. In fact, it would be a great wager. Let’s see how. Note that we merge a tie result in the expected loss equation for simplicity.
Expected value (EV) = wager + (expected win – expected loss)
In this scenario, on your point of view, it would look like this:Expected value (EV) = 1 + ((0.5 x 4) – (0.5 x 1)) => 2.5
This means that betting on team A in such a game would be extremely favourable. It would be like turning water into wine, except that in this case you would turn 1£ into 2.5£ on average.
Conclusions on Expected Value
We hope to have convinced you about the usefulness of the concept of Expected Value. It is one of the numerous tools in any gambler’s arsenal. It allows us to estimate what bets are profitable and which ones are not. Of course, it is not the end all be all. There are some games that we like and will continue to play even though in the long run we know that the house has an advantage. But it is a great concept that can be used to maximize wins and limit losses.